Derneğimiz Hakkında
| Merkez Bankası Döviz Kuru | |||
| ALIŞ | SATIŞ | ||
| USD | 0 | 0 | |
| EURO | 0 | 0 | |
1. GİRİŞ
1.1. Yeryüzünün Şekli
Yeryüzünün tamamının ya da bir kısmının şekil, büyüklük ve konum bakımından belirlenmesi jeodezinin amacını oluşturmaktadır. Yeryüzünün ölçülmesi, hesabı ve çiziminde kullanılan araç ve yöntemlerin incelenmesi de jeodezinin konusunu oluşturur.
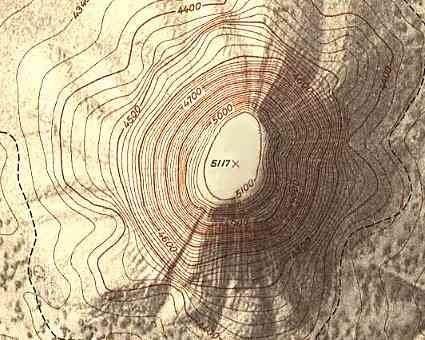
Yeryüzünün şekli, karaların altından da devam ettiği varsayılan denge halindeki deniz yüzeyinin oluşturduğu kapalı bir şekildir. Bu şekle geoit adı verilmektedir. Geoit, geometrik bir şekil değildir. Geoide en yakın geometrik şekil dönel elipsoittir.
Ölçme alet ve yöntemlerinde gerçek çekül doğrultuları (geoit normalleri) esas alınırlar. Geoit, her noktasında çekül doğrultusuna diktir. Çekül doğrultuları aynı noktalardaki elipsoit normalleri ile bir e açısı yaparlar; bu açıya çekül sapması denilir. Çekül sapmaları, geoitin yapısına göre çeşitli noktalarda farklı büyüklükte ve yöndedirler.

Şekil 1.1 Yeryüzünün şekli
1.2. İzdüşüm Yüzeyi
Ölçmeye ve izdüşüme temel oluşturan yüzeylerin bu farklı özellikleri, fiziksel yeryüzünün geometrik bir yüzey üzerine iz düşürülmesini karmaşık bir işlem haline getirmektedir. Geoit üzerindeki hesaplamaların güçlüğü nedeniyle, ölçülecek alanın büyüklüğüne bağlı olarak, konum ölçmeleri için yeryüzünün şekli; elipsoit, küre ya da düzlem olarak alınabilir. Yükseklik ölçmeleri için başlangıç (referans) yüzeyi olarak, ölçülecek alanın büyüklüğüne bağlı olmaksızın denge halindeki deniz yüzeyi, yani geoit alınır. Başlangıç yüzeyi olarak düzlemin alındığı ölçmeler; ölçme bilgisinin ya da topografyanın ilgi alanı içinde olmaktadır. Topografya, Yunanca kökenli bir sözcüktür ve yer yüzeyinin çizimsel tanımı anlamına gelir.
|
Ölçülecek Alanın Büyüklüğü |
Konum Ölçmeleri İçin Başlangıç Yüzeyi |
Yükseklik Ölçmeleri İçin Başlangıç Yüzeyi |
|
Büyük alanlar >5000 km2 |
Elipsoit |
Geoit |
|
Orta büyüklükte < 5000 km2 |
Küre |
Geoit |
|
Bölgesel < 10 km ´ 10 km |
Düzlem |
Geoit |
Çizelge1.1 Başlangıç yüzeyleri
1.3. Topografyanın (Ölçme Bilgisinin) Uygulama Alanları
Ölçme bilgisinin uygulama alanlarından bazıları şunlardır:
· Tapu ve kadastro
· Madencilik
· Şehircilik
· Belediye hizmetleri
· Tarım
· Ormancılık
· Askeri
· Kara, deniz, hava ulaşımı
· Haberleşme
· Turizm
· Yapı
· Enerji nakil hatları
· Doğal gaz, su, kanalizasyon hatları
· Mühendislik ölçmeleri
· Deformasyon ölçmeleri
· Bilgi sistemleri (coğrafi, arazi, kent vb.)
Topografya, ulaştırma amaçları için karayollarında, etüt, güzergah tespiti, zeminde yerin gezilmesi, şeritvari harita alımı, projelendirme ve projenin aplikasyonunda; deniz ulaşımında, sualtının hidrografik haritasının çıkartılması, limanlar ve kanallardaki ölçmelerde; hava ulaşımında da hava alanı inşaatında ve işaretlemelerinde, hava seyri için zeminde belirli hedeflerin tespitinde vb. çalışmalarda kullanılır.
Bu hizmetleri yerine getirecek teknik personel, haritacılardır (jeodezi ve fotogrametri mühendisleridir). Birçok mühendislik - mimarlık hizmetleri, tek bir disiplinin ilgi alanı olmaktan çıkmış, farklı disiplinlerin işbirliği içinde çalışmalarını zorunlu kılmaktadır. Topografya dersinin amacını, ölçme bilgisinin temel bilgilerini vererek, farklı disiplinler için ortak bir platform oluşturmak biçiminde özetleyebiliriz.
1.4. Bazı Kavram ve Tanımlar
Uygulamada sıkça karşılaşılan bazı kavramlar şunlardır:
HARİTA: Bir arazi parçasının, belirli bir ölçeğe göre küçültülmüş ve belirli bir projeksiyon sisteminde, özel işaretlerle kağıt üzerinde gösterilmiş şeklidir.
PLAN: Yeryüzündeki şekillerin yatay bir düzlem üzerindeki izdüşümleridir. Planlar belli bir ölçeğe göre çizilirler.
KROKİ: Bir arazi parçası ile üzerindeki doğal ve yapay tesisleri gösteren yaklaşık ölçekli bir taslaktır.
KESİT (PROFİL) : Yeryüzündeki şekillerin düşey bir düzlem üzerindeki izdüşümleridir.
İMAR PLANI: Bir şehrin doğal ve sosyal yapısını veri olarak alan, bu veriler arasındaki mekan ilişkilerini ve gelecekteki arazi kullanımına ait esasları gösteren, standart topografik kadastral haritalar üzerine çizilen planlardır. İmar planları, nazım imar planı ve imar uygulama planı olmak üzere iki gruba ayrılır.
Nazım İmar Planı: Halihazır durumu gösteren haritalar üzerine çizilen, kentin gelecekteki konut, ticaret, sanayi bölgelerini, yeşil alanları, ulaşım ağlarını vb. diğer arazi kullanışlarını ana çizgileriyle gösteren plandır.
İmar Uygulama Planı: Halihazır ve kadastral durumu gösteren haritalar üzerine, nazım imar planı esaslarına göre çizilen, çeşitli bölgelerdeki yapı adalarını, yollarını, inşaat düzenlerini, alt yapı tesislerini ve uygulama için gerekli diğer bilgileri gösteren plandır. Bu planlar, genellikle 1/1000 ölçeğinde yapılırlar.
PAFTA: Belirli bir bölümleme düzenine uygun olarak çizilen harita veya planların, birbirleriyle kenarlaşabilen parçalarından her biridir. Büyük ölçekli haritalarda standart pafta boyutları 70 ´ 90 cm din. Pafta kenarlarında 5 er cm boşluk bırakılır. Pafta, 10 cm aralıklarla karelere bölünür.
ADA: Dört tarafı sokak, cadde, meydan, demiryolu, akarsu vb. doğal ya da yapay engellerle çevrilmiş arazi parçasıdır.
İmar Adası: İmar planına uygun olarak oluşturulan parseller topluluğudur.
Kadastro Adası: Yeryüzünde halen mevcut olan kadastro parselleri topluluğudur.
PARSEL: Belli bir amaçla ayrılıp sınırlandırılmış arazi parçalarının her birisine parsel adı verilir.
ÇAP: Bir arazi parçasının ya da bir binanın zemindeki konumunu, sınırlarını ve boyutlarını göstermek için hak sahibine verilen belgedir.
İmar Çapı: Yerel idareler tarafından verilen, imar parselinin ve yapılacak binanın boyutlarını, yola uzaklığını, kat sayısını vb. bilgileri gösteren belgedir.
Kadastro Çapı: Kadastro müdürlükleri veya tapu sicil müdürlükleri tarafından verilen, kadastro parsellerinin sınırlarını, sahibini, yüzölçümünü vb. bilgileri gösteren belgedir.
PARSELASYON: İmar adalarının, imar planı ve imar yönetmeliği esaslarına uygun biçimde ve büyüklükte düzgün parsellere ayrılması için yapılan işlemdir.
APLİKASYON (UYGULAMA) : Haritadaki ya da plandaki bilgilerin zemine işaretlenmesi için yapılan işlemlerin tümüdür.
YÜKSEKLİK (KOT) : Yeryüzündeki bir noktanın, çekül doğrultusunda başlangıç yüzeyine (jeoide) olan uzaklığıdır.
PLANKOTE: Yapılan planların üzerine, noktaların başlangıç yüzeyine göre yüksekliklerinin yazılmasıyla elde edilen planlardır.
YÜKSEKLİK EĞRİLİ HARİTA: Planların üzerine, aynı yükseklikteki noktaların birleştirilmesiyle elde edilen eğrilerin çizilmesiyle oluşan planlardır.
HATA: Ölçü değerinden, gerçek değer ya da kesin değerin çıkartılması ile bulunur. Ölçüm, hesap ve çizim işlerinde yapılabilecek, kabul edilebilir en çok hata miktarına da hata sınırı (tolerans sınırı) denilir.
DÜZELTME: Hata ile ters işaretli olup, gerçek değer ya da kesin değerden ölçü değerinin çıkartılması ile bulunur.
1.5. Ölçek
ÖLÇEK: Haritadaki ya da plandaki uzunluğun arazideki uzunluğa oranıdır. Ölçek üç türlü ifade edilebilir (gösterilebilir).
Sayısal Ölçek: Payı 1 olan bayağı kesir biçiminde ifade edilir.
![]()
Olarak tanımlanır. Bu üç parametreden ikisi bilinirse üçüncüsü kolayca bulunabilir.
Büyük ölçekli harita ve planlarda, yeryüzünün küreselliği düşünülmeden, harita üzerinde yapılan ölçmeler, ölçeğin paydası ile çarpılarak yeryüzündeki değerleri bulunur. Örneğin 1/500 ölçekli bir haritada l = 87.4 mm’ lik bir uzunluğun arazideki karşılığı,
L = M ´ l
L=500 ´ 87.4=43700 mm =43.70 m
olur.
Çizgisel Ölçek : Özellikle küçük ölçekli haritalardaki uzunluğun arazideki karşılığını bulmak için kullanılır. Çizgisel ölçek bir doğru üzerinde gösterilir. Bu doğrunun üzerinde bir sıfır noktası işaretlenir. Sıfır noktasından itibaren sağa doğru, ölçeğe göre yuvarlak değerler veren (10m, 20m, 50m, 100m,...) bölümler alınır. Sıfır noktasından itibaren sola doğru da sağdaki 1 bölüm genişliği kadar alınarak, daha küçük bölüm değerleri bu aralıkta işaretlenir. Uzunlukların bulunmasında iki ucu sivri bir pergelden yararlanılır.

Şekil 1.2 Çizgisel ölçek
Harita üzerinde arasındaki uzunluğu ölçülmek istenen iki noktaya, pergelin uçları yerleştirilerek, pergelin, iki nokta arasındaki uzunluk kadar açılması sağlanır. Pergelin bu ayarı bozulmadan, uçlardan biri kesirli ölçek kısmına rastlayacak şekilde, diğer uç uygun bir tam bölüm çizgisine çakıştırılır. Uzunluğun, yuvarlak değerleri, sıfır noktasının sağındaki tam bölümden, daha küçük birimleri ise sıfır noktasının solundaki kesirli kısımdan okunur. Yukarıdaki örneğimizde, pergelin bir ucu 200 tam bölüm çizgisine tatbik edilmiş, diğer ucu ise kesirli kısımda 25 m’lik kısma isabet etmektedir. Bu durumda bu iki nokta arasındaki uzunluk 225 metredir.
Geometrik Ölçek: Çizgisel ölçeğe benzemekle birlikte ondan biraz daha farklıdır. Çizgisel ölçekte, tahminle okunan alt birimden daha küçük değerler, geometrik ölçekte doğrudan okunabilmektedir. Geometrik ölçeğin oluşturulması için, önce çizgisel ölçek oluşturulur. Çizgisel ölçeğe paralel olarak uygun aralıklarla 10 adet çizgi çizilir. Çizgisel ölçek üzerindeki tam bölümlerden dikler çıkılır. Sıfırın solundaki küçük bölüm çizgileri, en üstteki yatay çizgi üzerinde de işaretlenir ve şekilde görüldüğü gibi 1 birim kaydırılarak, çizgisel ölçek üzerindeki işaretlerle birleştirilir. Bu şekilde geometrik ölçek elde edilmiş olur.

Şekil 1.3 Geometrik ölçek
Haritadan sivri uçlu pergelle alınan uzunluğun, arazideki karşılığını bulmak için, pergelin uçlarından biri sıfır noktasının solundaki ondalık kısımda kalacak şekilde diğer uç, tam bölüm çizgilerinden birine çakıştırılır. Pergelin ondalık kısımdaki ucu, eğik çizgilerden biri ile çakışıncaya kadar pergelin iki ucu da yatay çizgilere paralel kaydırılır. İki nokta arasındaki uzunluk, L= a + b + c biçiminde elde edilir. Örneğimizde, L= 260 m +3 m +0.6 m = 263.5 metredir.
Herhangi bir şeklin alanı, bir dikdörtgenin alanı biçiminde ifade edilebilir. Kenarları a ve b olan bir dikdörtgenin haritadaki f alanı, f = a * b dir. Haritadaki bu f alanına karşılık gelen arazideki alanı (F) bulmak için dikdörtgenin kenarları, ölçeğin paydası ile çarpılırsa;
F = a * M * b * M =a * b * M2 = f * M2
olur. Buradan da
![]()
bağıntısı elde edilir. Haritadaki alanı ( f ) verilen bir şeklin, arazideki alanı ( F ) bu bağıntı ile bulunur. Bu eşitlik alansal ölçek olarak ifade edilmektedir.
Haritaların çiziminde gösterilen tüm özen ve dikkate karşın yine de kaçınılamayan hatalar vardır. Bu hataya çizim hassasiyeti (çizim inceliği) denilmektedir. Normal insan gözü, 1 milimetrenin beşte birini ayırt edebilir. Bu nedenle, çizim inceliği 0.2 mm olarak kabul edilir ve hesaplanan değerler, ölçeğin paydası ile 0.2 mm’nin çarpımı kadar hatalı olabilir. Örneğin 1/1000 ölçekli bir haritada çizim inceliği; 0.2 mm * 1000 =200 mm = 20 cm olur.
Örnek 1: Arazide 125.00 m olarak ölçülen bir uzunluk, haritada 6.25 cm olarak ölçülüyor. Bu haritanın ölçeğini bulunuz.
![]()
![]()
olarak bulunur.
Örnek 2: 1/500 ölçekli bir haritadaki alanı f=345 mm2 olan parselin, arazideki alanını bulunuz.
![]()
Bu parselin arazideki alanı 86.25 m2 dir.
Haritaların Ölçeklerine Göre Sınıflandırılması
Haritalar, ölçeklerine göre üçe ayrılabilir:
a) Büyük Ölçekli (1/200 - 1/5000 ) Haritalar:
Bunlardan 1/200 -1/2000 ölçekli olanlara plan denilir. Büyük ölçekli haritalar, çoğunlukla kadastro, imar-planlama, kamulaştırma, kamu alt yapıları, arazi toplulaştırması, orman ve madencilikte kullanılır.
b) Orta Ölçekli (1/10.000 - 1/50.000) Haritalar
Genellikle askerlikte taktik amaçlar için hazırlanan bu haritalar, topografik özellikte olduğundan bölge ve nazım imar planlamasında, ulaşım etütlerinde kullanılır.
c) Küçük Ölçekli (1/100.000 den küçük) Haritalar
Bunlar coğrafya ve dünya haritalarıdır. Daha az ayrıntı içerir ve genel amaçlar için, örneğin kara, deniz, hava trafiğinde vb. işlerde yararlanılır.
1.6. ÖLÇÜ BİRİMLERİ
Uzunluk ölçü birimi olarak metre kullanılmaktadır. Alan ölçüsü birimi metrekaredir ve kısaca m2 şeklinde gösterilir. Uygulamada aşağıdaki alan ölçümü birimleri de kullanılmaktadır.
1 Ar (a) = 102 = 100 m2
1 Dekar (dek) = 103 = 1000 m2 = 1 dönüm
1 Hektar (ha) = 104 = 10.000 m2 =10 dönüm
Hacim ölçümü birimi, metreküptür ve kısaca m3 şeklinde gösterilir. Bu birim, yol, tünel ve benzeri kazı (hafriyat) işlerinde kazılan toprağın miktarını belirlemekte kullanılır.
1.6.1. Açı Birimleri
a- Derece
Tam bir daire çevresinin 360 da birini gören merkez açıya 1° (derece) denir.
1° = 60' (derece dakikası)
1¢ = 60" (derece saniyesi)
Hesap makinesi ile işlem yaparken, açıların yalnızca derece biçiminde olması gerekir. Aksi takdirde hesap makinesi ile yapılan işlemler hatalı olur. Eğer açı, derece, dakika, saniye biçiminde verilmişse, öncelikle bu dakika ve saniyelerin dereceye dönüştürülmesi gerekir. Daha sonra yapılması gereken işleme geçilir.
Örnekler:
Derece, dakika, saniye biçiminde verilen açının derece biçimine dönüştürülmesi.
15° 14' 51" = 15° +14' +(51/60)' = 15° +14' +0'.85 = 15° +14'.85 = 15°+(14'.85/60)°
= 15° +0°.2475 = 15°.2475
Derece cinsinden verilen açının derece, dakika, saniye biçimine dönüştürülmesi.
15°.2475 =15° 14' 51" (0.2475 * 60 = 14'.85; 14'.85 -14' = 0'.85 ; 0'.85*60 = 51")
86°.9382 = 86° 56' 17".52 (0°.9382*60=56'.292; 56'.92-56'=0'.292; 0'.292*60=17".52)
Bu işlemler hesap makinelerinde bulunan hazır tuşlar yardımı ile kolayca yapılabilir. Örneğin CASIO FX-880P de yukarıdaki örnekler şu şekilde yapılabilir:
DMS$( 15.2475 ) EXE 15°14'51"
DMS$( 86.9382 ) EXE 86° 56' 17".52
DEG( 15,14,51 ) EXE 15°.2475
DEG( 86,56,17.52 ) EXE 86°.9382
b- Grad (Gon)
Tam bir daire çevresinin 400 de birini gören merkez açıya 1g (grad veya gon ) denir.
1g = 100c
1c = 100cc
Örnekler:
56g.7284 =56g 72c 84cc
105g 36c 89cc =105g.3689
c- Radyan
Tam bir daire çevresinin 2p de birini gören merkez açıya 1 radyanlık açı denir ve r (ro) ile gösterilir. Başka bir söyleyişle, yarıçap uzunluğundaki yayı merkezde gören açıya 1 radyanlık açı denir. Bir çemberde yarıçap uzunluğundaki yay parçası, 1 radyanlık yaydır. 1 radyanlık açının grad ya da derece cinsinden karşılığını hesaplamak için, R=1 yarıçaplı çemberde çevre 2p olduğu dikkate alınarak,
 |
rg=400/2p =200/p = 63g.6620 (1 radyanlık yayın grad cinsinden karşılığı)
rc= rg ´ 100 = 6366g.20 (1 radyanlık yayın grad dakikası cinsinden karşılığı)
rcc= rc ´100 =636620g (1 radyanlık yayın grad saniyesi cinsinden karşılığı)
r°=360/2p =180/p = 57°.29578 (1 radyanlık yayın derece cinsinden karşılığı)
r'= r° ´ 60 = 3437'.747... (1 radyanlık yayın derece dakikası cinsinden karşılığı)
r"= r' ´60 = 206 264".806 (1 radyanlık yayın derece dakikası cinsinden karşılığı)
Bir açının radyan değeri genel olarak,
![]()
ile bulunur. a radyan açının derece ve grad cinsinden karşılıkları,
![]()
şeklinde, a açısını daire merkezinde gören b yay uzunluğu ise,
![]()
eşitliği ile bulunur.
d- Milyem
Bir daire çevresinin 6400 ‘de birini merkezde gören açıya milyem denir. 1 milyem, 1 km uzaklıkta yaklaşık olarak 1 m’lik bir yaya karşılık gelir. Bu açı birimi, bilimsel çalışmalarda kullanılmaz. Daha çok askerlikte (top atışlarında) kullanılır. Rakamın sağ üst köşesinde küçük bir yatay çizgi ile gösterilir.
1600¯ =90o = 100g
1.6.2. Açı Birimlerinin Birbirine Dönüştürülmesi
400g =360° = 2p radyan ya da 200g = 180° = p radyan ve
![]()
eşitliklerinden yararlanılır.
1- Derecenin Grada çevrilmesi
![]()
Verilen açının dakika ve saniyesi, derece cinsine çevrildikten sonra 10/9 ile çarpılır.
Örnek: 156° 43' 55" nin grad cinsinden değeri,
156° 43' 55" = 156° + 43' + (55/60)' =156° 43'.91667 = 156° + (43.91667/60)° = 156°.73194
156°.73194 ´ 10/9 = 1567.3194/9 = 174g.1466
Aynı işlem CASIO FX-880P ile
DEG( 156,43,55 ) EXE 156°.73194 ´ 10 / 9 = 174g.1466
şeklinde bulunur.
2- Derecenin Radyana Çevrilmesi
![]()
Bunun için derece cinsinden verilen açının r ile bölünmesi gerekir.
a = a° /r° = a¢/r¢ = a²/r²
Örnek: 156° 43’ 55” in radyan cinsinden değeri;
156°43’55” = 156°.73194 değeri, r° = 57.29578 ile bölünerek,
a = 156.73194 / 57.29578 = 2.735488
radyan bulunur.
3- Gradın Dereceye Çevrilmesi
![]()
Verilen açı, 9/10 = 0.9 ile çarpılarak derece cinsine dönüştürülür.
Örnek: 187g.4892 nin derece cinsinden değeri,
187.4892 * 0.9 = 168°.74028 = 168° 44’ 25”.01
şeklinde bulunur.
4- Gradın Radyana Çevrilmesi
![]()
a = ag/rg = ac/rc =acc/rcc
Örnek: 149g.5824 ün radyan cinsinden karşılığı,
a = 149.5824 / 63.6620 = 2.349634 olur.
5- Radyanın Dereceye Dönüşümü
![]()
Radyan cinsinden verilen açı, rO ile çarpılarak derece cinsinden değeri bulunur.
Örnek: 1.586327 radyanın dereceye dönüşümü,
a° = 1.586327 ´ 57.2958 = 90.8899
a = 90° + (.8899 ´ 60)¢ = 90°+ 53’.394 = 90° + 53¢ + (.394 60) ¢¢ = 90°53¢23¢¢.64
6- Radyanın Grada Dönüşümü
![]()
Radyan cinsinden verilen açı, rg ile çarpılarak grad cinsinden değeri bulunur.
Örnek: 0.078952 radyanın grad karşılığı;
ag = 0.078952 ´ 63.6620 = 5g.0262 =5g 02c 62cc şeklinde bulunur.
1.7. ÖLÇÜ HATALARI VE HATALARIN YAYILMA ESASLARI
Teknik çalışmalarda ölçme sonuçları önemli rol oynadığından ölçü inceliğinin bilinmesi gerekir. Değişik nedenlerden ileri gelen ölçü hataları genel olarak 3 grupta toplanabilir:
1- Kaba Hatalar: Ölçme aletindeki yanlış okuma hatası, yanlış hedefe bakmaktan doğan hatalar gibi kontrol ölçmeleriyle ortaya çıkarılabilecek hatalardır.
2- Düzenli (Sistematik) Hatalar: Ölçme sonuçlarına aynı yönde etkiyen hatalardır. Örneğin, aletin ayarının bozuk olması, hava sıcaklığının etkisinin dikkate alınmaması gibi hatalardır.
3- Düzensiz (Tesadüfi) Hatalar: Kaba ve düzenli olmayan diğer bütün hatalar düzensiz olarak adlandırılırlar ve bu hatalar, kontrol ölçmeleriyle de ortaya çıkartılamaz.
1.7.1. Gerçek Hata, Görünen Hata ve Düzeltme
Gerçek hata ( -ei ), ölçü değerinden (Li ) gerçek değerin (X ) çıkartılmasıyla bulunur.
-ei = Li - X
Gerçek düzeltme, gerçek hatanın ters işaretlisidir ve
ei = X - Li
bağıntısı ile belirlenir. Gerçek değer, hatasız ölçü yapılamayacağı için genellikle bilinmez. Bazı durumlarda tanım gereği bilinir. Örneğin, bir üçgenin iç açılarının toplamı 180° dir.
Bir büyüklüğe ait L1, L2, ...,Ln ölçü dizisinden yararlanılarak gerçek değere yakın olduğuna inanılan bir görünen değer tarif edilir. Ölçülerin aritmetik ortalaması,
![]()
bağımsız ölçülerin her birinden gerçek değere çok daha yakındır. Bu şekilde elde edilen değere Kesin Değer denilir. Gerçek hataya benzer şekilde, kesin değer yardımı ile bir görünen hata tanımı,
Görünen Hata = Li - L = -vi
bağıntısı ile ifade edilir. Burada vi düzeltmedir ve hata ile ters işaretlidir.
vi = L - Li
bağıntısıyla ifade edilir. Görünen hataların toplamı sıfırdır. Hata ve düzeltmeyi kısaca,
Hata = Ölçü değeri – kesin değer
Düzeltme = Kesin değer – ölçü değeri
biçiminde özetleyebiliriz.
1.7.2. Karesel Ortalama Hata (m)
Gauss tarafından tanımlanan karesel ortalama hataya çoğu zaman sadece Ortalama Hata da denir. Bir ölçünün ortalama hatası
![]()
eşitliği ile elde edilir. Görünen hataların kullanılması durumunda bir ölçünün ortalama hatası,
![]()
ifadesi ile bulunur. Kesin değerin ortalama hatası ise
![]()
eşitliği ile bulunur.
1.7.3. Mutlak Hatalar Ortalaması (t)
n tane ölçünün hatalarının mutlak değerleri toplamının, n ölçü sayısına bölünmesiyle elde edilir.
![]()
m > t olduğundan doğruluk tespitinin derecesinin tespitinde m kullanılır.
1.7.4. Muhtemel Hata (r)
Hatalar mutlak değerlerine göre sıraya dizilir. Ortadaki hata, muhtemel hatadır.

n ® ¥ iken t = 4/5 m , r = 2/3 m
t : m : r = 0.80 : 1 : 0.67
Örnek :
![]()
![]() ε ε
ε ε
0 0
3 3
4 5
5 = r 7 ü r = 8
7 9 þ
8 11
11 12
14
1.7.5. Bağıl (Rölatif) Hata
Karesel ortalama hatanın, kesin değere oranı bağıl hata olarak adlandırılır. Payı 1 olacak şekilde bir kesir oluşturulur. Örneğin, 3 km lik bir uzunluk ±3 cm incelikle ölçülmüşse, bunun bağıl hatası,
![]()
1.7.6. Hataların Yayılma Yasası
L1, L2, ......,Ln bağımsız değişkenler olsun. Yani her biri bir ölçü grubundan elde edilmiş değerler ise ve bu bağımsız değişkenlerin ortalama hataları da m1, m2, m3,.....,mn olmak üzere
F = F(L1, L2, .....,Ln)
fonksiyonunun ortalama hatası,

bağıntısından elde edilir. Burada ![]() , fonksiyonun Li değişkenine göre kısmi (parsiyel) türevidir. Bu bağıntının çıkarılmasında
, fonksiyonun Li değişkenine göre kısmi (parsiyel) türevidir. Bu bağıntının çıkarılmasında

toplam diferansiyelinden yararlanılır.
ÖRNEKLER:
1- Bir açı 5 kez ölçülmüş ve aşağıdaki değerler elde edilmiştir. Bir ölçünün ortalama hatası ile kesin değerin ortalama hatasını bulunuz.
Li = L0 + DLi denilir ve L0 = 50g .85 00 alınırsa,
![]()
Li Vi = L - Li Vi 2
50g.85 20 +4cc 16
50. 85 27 -3 9
50. 85 24 0 0
50. 85 30 -6 36
50.85 19 +5 25
[V] = 0 [Vi 2 ] = 86
Bir ölçünün ortalama hatası m,
![]()
Kesin değerin ortalama hatası ML,
![]()
olur. Kesin değer ve ortalama hatası, L=50g.8524 ± 2cc şeklinde de yazılabilir.
2- Bir üçgenin açıları a=75g.67 43 ± 8cc ve b=83g.96 22 ±10cc olduğuna göre g açısını ve bu açının ortalama hatası mg yı bulunuz.
g = 200g - (a+b) = 200 -(75.67 43 + 83.96 22) = 40g.36 35
Bu fonksiyona hata yayılma kanunu uygulanırsa,
dg = - da - db


![]() 3- Dikdörtgen şeklindeki bir parselin kenarları L1 ve L2 dir.
3- Dikdörtgen şeklindeki bir parselin kenarları L1 ve L2 dir.
Bu parselin alanının ortalama hatasını bulunuz.
![]() F = L1 L2
F = L1 L2
dF = L2 dL1 + L1 dL2

Not: Alan hesaplarında sonuca; küçük kenardaki hata, büyük kenardaki hatadan daha çok etki eder.
![]()
![]() 4- (P1P) = a ve P1P=S bilindiğine göre P noktasının ortalama
4- (P1P) = a ve P1P=S bilindiğine göre P noktasının ortalama
![]() konum hatasını bulunuz.
konum hatasını bulunuz.
![]()
![]()
 Verilenler: a, ma, S, ms
Verilenler: a, ma, S, ms
![]()
![]()
![]() İstenenler: mP = ?
İstenenler: mP = ?
![]()
![]() Y= S sina dy=sina ds + S cosa da
Y= S sina dy=sina ds + S cosa da
X= S cosa dx=cosa ds - S sina da

Sayısal Örnek: S=100.25 m ±0.04 m; a= 58g.14 70 ± 40cc olduğuna göre P noktasının ortalama konum hatasını bulunuz.
![]() = 0.0016 + 0.00003968 = 0.00163968
= 0.0016 + 0.00003968 = 0.00163968
mp= ± 0.0405 @ ± 0.04 m = ± 4 cm
 5- S=50 m ± 2 cm , a=50g ± 1c olduğuna göre mh = ?
5- S=50 m ± 2 cm , a=50g ± 1c olduğuna göre mh = ?
![]()
|
|

6- Bir uzunluk 3 parçaya bölünerek elde edilmiştir. Birinci parçanın ortalama hatası m1 = ±1 cm, ikinci parçanın ortalama hatası m2 = ± 2 cm ve üçüncü parçanın ortalama hatası da m3 = ±4 cm olduğuna göre toplam uzunluğun ortalama hatasını bulunuz.

![]()

 |
7- c = 415.42 m +0.05 m
g = 42g.1430 + 20cc
b = 85g.3657 + 20cc
b = ?
mb = ?


mb = 0.0062732+0.0000234+0.0007038=0.0070
mb = +0.07 m = + 7 cm
Okunma Sayısı: 2111
DİĞER HABERLER
- Yıllık Faaliyet Formu Örneği
- İş Sözleşme Örneği
- Şifalı Bitkiler Sözlüğü
- Kaza Tespit Tutanağı
- Asgari Geçim İndirim Formu
- Burs Başvuru Formu
- DEMİR METRAJ TABLOSU
- HAKEDİŞ PROGRAMI
- NETCAD 3D
- autocad eğitimi 1
- autocad eğitimi 2
- autocad eğitimi 3
- autocad eğitimi 4
- autocad eğitimi 5
- autocad eğitimi 6
- autocad eğitim 7
- autocad eğitim 8
- 3D YOL PROGRAMI CİHAZA GİRİŞ
- ÜYELİK FORMU





